微分方程是解決很多復(fù)雜問題的關(guān)鍵理論。微分方程這個看似高深莫測的數(shù)學(xué)概念，為何被眾多數(shù)學(xué)家贊譽為數(shù)學(xué)的靈魂，成為了很多數(shù)學(xué)家一直都在思考的問題，微分方程是描述事物變化率的數(shù)學(xué)工具。在現(xiàn)實世界中，許多現(xiàn)象都可以通過微分方程來精確描述。物體運動時的速度和加速度可以用微分方程表示；電路中的電流和電壓也可以通過微分方程來描述。正是這種與現(xiàn)實世界緊密相連的特性，使得微分方程成為數(shù)學(xué)中的核心內(nèi)容。

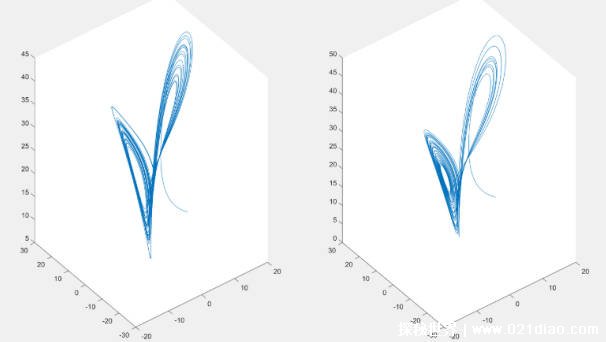
解決復(fù)雜問題的關(guān)鍵

在科學(xué)、工程和經(jīng)濟學(xué)等領(lǐng)域，我們經(jīng)常面臨一些復(fù)雜的問題，這些問題往往涉及到多個變量之間的相互作用。而微分方程能夠?qū)⑦@些復(fù)雜的相互作用簡化為可理解的數(shù)學(xué)模型，從而幫助我們找到解決問題的方法，在經(jīng)濟學(xué)中，微分方程被用來描述市場的供需關(guān)系，為政府制定經(jīng)濟政策提供依據(jù)。

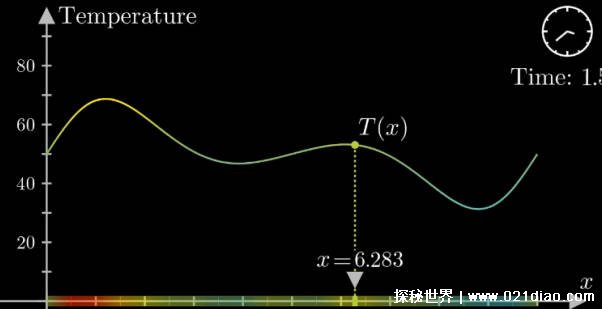
推動數(shù)學(xué)發(fā)展的動力

微分方程不僅在實踐應(yīng)用中發(fā)揮著重要作用，更是推動數(shù)學(xué)理論發(fā)展的重要動力。通過研究微分方程的性質(zhì)和解法，數(shù)學(xué)家們不斷拓展數(shù)學(xué)理論體系，推動了數(shù)學(xué)學(xué)科的整體發(fā)展。許多著名的數(shù)學(xué)家，如牛頓、萊布尼茨和歐拉等，都是因為對微分方程的研究而取得了卓越的成就。

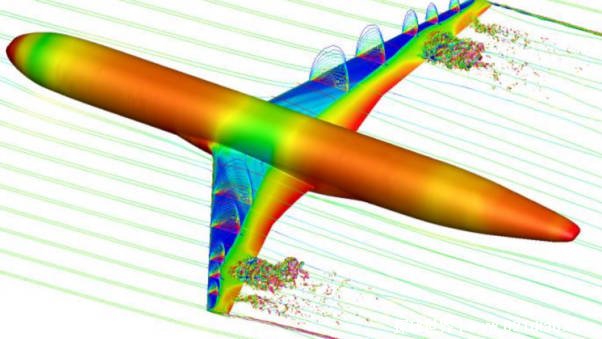
緊密相連

微分方程以其獨特的魅力將數(shù)學(xué)與現(xiàn)實世界緊密相連。它既能幫助我們解決實際問題，又是推動數(shù)學(xué)發(fā)展的關(guān)鍵力量。應(yīng)當(dāng)深入學(xué)習(xí)和研究微分方程，以便更好地理解這個世界，并解決我們面臨的復(fù)雜問題，才能真正領(lǐng)略到微分方程所蘊含的無窮魅力。