施瓦茲燈籠的理論挑戰了科學家對幾何數學的認知。數學怪獸這個詞可能會讓人想到一些高深莫測、難以理解的數學概念,這個詞被用來形容一種簡單而美麗的數學結構施瓦茲燈籠。施瓦茲燈籠是一種由三個等邊三角形構成的幾何結構。它看起來像一個燈籠因此得名。盡管它看起來非常簡單,但施瓦茲燈籠卻具有令人驚嘆的數學性質,被形容為數學怪獸。

不定向幾何體
施瓦茲燈籠是一個不可定向的幾何體。這意味著它無法被定向,使得其內部和外部在視覺上無法區分。這與其他幾何體如球體或立方體不同,它們的內部和外部是可區分的。施瓦茲燈籠的不可定向性質使其成為一個有趣的數學研究對象。其次施瓦茲燈籠具有自相似性。這意味著它的形狀在各個尺度上都是相似的。
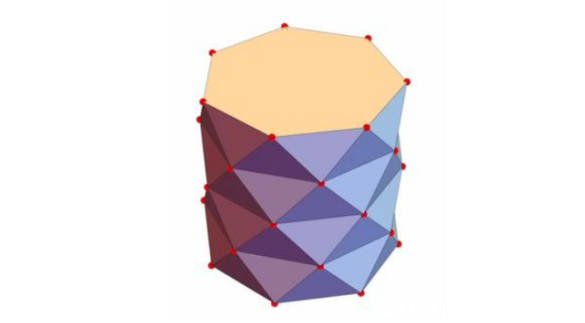
重復形狀
當你放大或縮小施瓦茲燈籠時,你會看到相同的形狀重復出現。這種自相似性是許多復雜數學結構和自然現象的共同特征,例如分形和混沌理論。這也與一些重要的數學問題緊密相關,它可以用來描述三維空間中的幾何對象,如曲面和流形。此外施瓦茲燈籠與一些重要的數學概念和定理有關,如歐拉公式和龐加萊猜想。
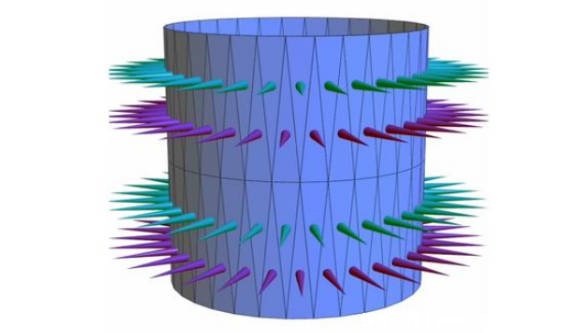
美麗復雜的數學
施瓦茲燈籠被稱為數學怪獸的原因還在于它具有許多令人驚訝的性質和與數學的緊密聯系。盡管它是一個相對簡單的幾何結構,但它在數學領域中卻引起了廣泛的興趣和研究。它的不可定向性和自相似性使它成為理解更復雜數學結構和自然現象的有趣工具。同時它也提醒我們,數學的美麗和復雜性可以在最簡單的形狀中找到。






















